The circle is a two-dimensional shape, which possesses its area and perimeter. The perimeter of the circle is also termed as the circumference, which is the measure around the circle. The area of the circle is the region defined by it in a 2D plane.
A circle is also termed as the locus of the points drawn at equidistant levels from the centre. The measure from the centre of the circle to the outer line is its radius. Diameter is the line that separates the circle into two equal parts and is also equal to twice the radius. A circle is a fundamental shape that is measured in terms of its radius.
In geometry or mathematics, a circle can be defined as a special variety of ellipse in which the eccentricity is zero and the two foci are coincident. It is easy to go from the area of a triangle to the area of a regular polygon by breaking the polygon into triangles and summing the areas of the triangles. But we need to first review the formula for the area of a polygon for reference. It can be shown that every regular polygon can be inscribed in a circle. If we draw a perpendicular line from the center of the circle to any side of the inscribed polygon, that line is called an apothem. It is a fact that the area of a regular polygon is $1/2ap$ where $a$ is the apothem and $p$ is the perimeter of the polygon.
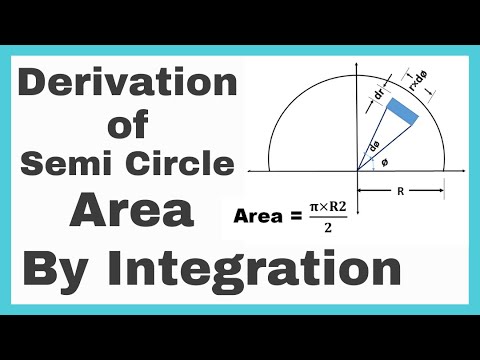
It is also a fact that as the number of sides of the inscribed regular polygons increases, the lengths of the apothems of the polygons approach the radius of the circle. The other way to derive the formula for the area of a circle is by dividing the circle with radius 'r' into several concentric circles and then spreading the lines, thus forming a triangle. The base of the triangle will be equal to the circumference of the circle, and the height equal to the radius of the circle.
Pies, cakes, pizzas; so many foods we eat neatly lend themselves to mathematics, because they are models of circles. Bits cut off by connecting any two points on the circle are segments. Since both sectors and segments are part of a circle's interior, both have area.
The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig. The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle. Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r.
The standard asks for "informal" derivations of this formula, and this task lets students both play and convince themselves. Instructors are encouraged to help any struggling students continue the process by making more drawings or by more carefully labeling pieces of the drawing (e.g., the radius). Alternatively, a more hands-on version of this task can be made by having students cut circles into wedges and reassemble the wedges themselves. An outline can be found on the NCTM illuminations page. A circle is the set of points in a plane that are equidistant from a given point . The distance from the centeris called the radius, and the point is called the center.
The angle a circle subtends from its center is a full angle, equal to or radians. We usually measure angles in degrees, for example, 90° in a right-angle, or 360° is a full revolution. This is mainly for historical reasons — the Babylonians used a base-60 number system and for example we still use 60 minutes in a degree. Radian measure is crucial in later work on calculus.
The idea is to define an angle so its size is the same as the size of the arc subtends it at the centre in a circle of unit radius. An alternative system is to measure angles in radians. From point B, on the circle, draw another circle with center at B, and radius OB.
The intersections of the two circles at A and E form equilateral triangles AOB and EOB, since they are composed of 3 congruent radii. Extend the radii forming these triangles through circle O to form the inscribed regular hexagon with 6 equilateral triangles. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. Cover the circle with concentric circles of "r" radius.
After dividing the circle along the designated line shown in the above figure and spreading the lines, the outcome will be a triangle. The base of the triangle will be equivalent to the circumference of the circle, and its height will be identical to the radius of the circle. An area of a circle is defined as a space occupied by the circle in a two-dimensional plane.A circle is an important geometric figure. We see circular objects around us in our everyday life, such as a bangle, a coin, a bike wheel, etc.
To know more about circles, we must understand the terms related to circles, like radius, diameter, perimeter, area of the circle, etc. One such important parameter, the area of a circle, is the region occupied by a circle in two dimensions. Fill the circle with radius r with concentric circles. After cutting the circle along the indicated line in fig.
4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle. He did prove that the area of a circle equals the area of a right triangle whose base is the circumference and whose height is the radius. This proof does not use limits - just Euclidean geometry. The following table gives the formulas for the area of sector and area of segment for angles in degrees or radians. Scroll down the page for more explanations, examples and worksheets for the area of sectors and segments.
Here, we will discuss the perimeter and area of circles in detail. I am going to discuss these axioms in a moment, but first let me show how Claim follows. But by Axiom 1 the length of the arc $PBQ$ is greater than $PQ$, while it follows from Euclid III.2 that $OB$ is greater than $OA$. Applying symmetry, this implies Claim in this case, and ought to suggest how the reasoning goes in general. The sectors are pulled out of the circle and are arranged as shown in the middle diagram. The length across the top is half of the circumference.
When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram. As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left. When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area. This area is the region that occupies the shape in a two-dimensional plane. So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle.
Now how can we calculate the area for any circular object or space? In this case, we use the formula for the circle's area. A perimeter of closed figures is defined as the length of its boundary. When it comes to circles, the perimeter is given using a different name. This circumference is the length of the boundary of the circle. If we open the circle to form a straight line, then the length of the straight line is the circumference.
To define the circumference of the circle, knowledge of a term known as 'pi' is required. The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius.
This suggests that the area of a disk is half the circumference of its bounding circle times the radius. The areas of both segments and sectors can be calculated in square units of whatever linear measurement you are given. The area of the circle is the measure of the space or region enclosed inside the circle. In simple words, the area of a circle is the total number of square units inside that circle. Radians In a circle of radius 1 unit, the angle subtended at the centre of the circle by the arc of length 1 unit is called 1 radian, written as 1 rad. This page describes how to derive the formula for the area of circle by using different methods.
The formula can be derived by using a number of methods ౼ some of them require the use of basic calculus while some other are just based on simple mathematics. In this post we are going to discuss some of those which are based on calculus. The animation starts with a circle with the radius and the circumference (2π r in red). The circumference unwraps to form a straight line and the circle opens up like the petals of a flower. The segments derived from the circle end up arranged along the ground like the teeth of a saw.
The left hand block of segments then move across to interdigitate with the right hand block of segments to form a rectangle. This labelled graphic helps us to understand one way of deriving the formula for the area of a circle (π r2). Next, we will look at the formula for the area of a sector where the central angle is measured in radians. Recall that the angle of a full circle in radians is 2π. A circle is a closed shape formed by tracing a point that moves in a plane such that its distance from a given point is constant.
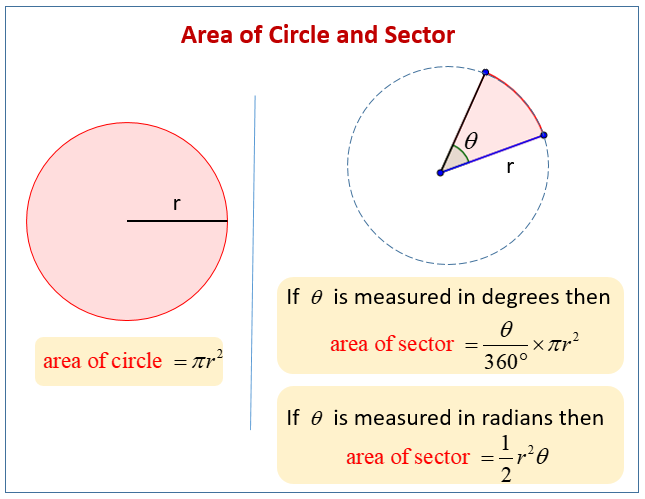
The word circle is derived from the Greek word kirkos, meaning hoop or ring. In this article, we cover the important terms related to circles, their properties, and various circle formulas. The full circle has angle \(2\,\pi \) radians around the centre. So, the area of the sector with a central angle \(\theta \) and having radius \(r\) will be proportional to this angle. The larger is the angle \(\theta ,\) the larger will be the area. This is shown by the shaded region in the figure above.
We then sum these slices between an angle of and . But, when using calculus, we do not use degrees, but rather we have to use radians, which as I explained in this blog, are a more natural unit for measuring an angle. The proof of this theorem in the extant version immediately follows its statement. I'll sketch it below, with a bit of explanation and a few more figures added.
The basic idea is almost exactly the same as that of Euclid's proof of Theorem XII.2, which asserts that the area of a circle is proportional to the square of its radius. The overlap of Archimedes' argument with that of Euclid should not be surprising, since Euclid's Theorem XII.2 is an immediate consequence of Archimedes'. The perimeter of circle is nothing but the circumference, which is equal to twice of product of pi (π) and radius of circle, i.e., 2πr. As we know, the area of circle is equal to pi times square of its radius, i.e. π x r2. To find the area of circle we have to know the radius or diameter of the circle.
Hence, the concept of area as well as the perimeter is introduced in Maths, to figure out such scenarios. But, one common question that arises among most people is "does a circle have volume? Since a circle is a two-dimensional shape, it does not have volume. In this article, let us discuss in detail the area of a circle, surface area and its circumference with examples.
Imagine you have a circle of radius r, and you make the radius a liiiittle bit bigger by adding dr to it. Comparing the area of sector and area of circle, we get the formula for the area of sector when the central angle is given in radians. We can calculate the area of the sector, given the central angle and radius of circle.
Recognize the below figure, if we divide up the circle into smaller sections and organise them in a systematic manner. When the circle is split into even smaller sectors, it progressively takes the shape of a rectangle. The more the number of sections the more it tends to have a shape of a rectangle as shown below. A central angle is the angle formed when two-line segments meet such that one of the endpoints of both the line segment is at the center and another is at the boundary of the circle. Let the given circle be divided into 16 equal sectors and then arranged approximately in the form of a parallelogram.
The total area of the circle will be equal to the total areas of the parallelogram. Since each sector has an equal area, each sector will have an equal arc length. Taken together, half of the circle is represented using one color and the other half using another color. The higher the number of sectors, the more the figure looks like a parallelogram with length equal to πr and breadth equal to r. The area of a circle can be calculated using three different formulas. The formulas are used based on whether the radius, diameter, or circumference is known to us.
Each of the three situations is discussed below with their formulas and solved examples. Is made up of a large number of concentric circular pieces of very thin string. The first step is to approximate the area of a circle using a regular polygon. We inscribe a regular polygon in the circle and split up the polygon into congruent isosceles triangles as shown below. Knowledge of area and perimeter of squares, rectangles, triangles and composite figures.
Where is the ratio of the diameter of a circle to its circumference, and is the radius of the circle. But, how would we go about proving this well known formula? To do so, we can use something called integration, which is a branch of calculus. The same rectangle is present four times in the circle .
By adding all areas of the rectangles and multiplying this by four, we can approximate the area of the circle. In our example we fit five rectangles into the circle. Is called the circumference and is the linear distance around the edge of a circle.